Q. 1. Let f:R -> Range of f given by f(x)= (x+1)2 - 1 and 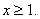 The set S = {x: f(x) = f -1(x)} is
The set S = {x: f(x) = f -1(x)} is
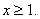 The set S = {x: f(x) = f -1(x)} is
The set S = {x: f(x) = f -1(x)} is - {0, -1}
- {0, 1}
- {-1, 1}
- {1, 1}.
Q. 2.
The minimum number of elements that must be added to the relation R = {
(1,2), (2,3) } on the set of natural numbers so that it is an
equivalence is
- 4
- 7
- 6
- 5
Q. 3. Let ‘R’ be a reflexive relation on a finite set ‘A’ having ‘n’ elements and let there be ‘m’ ordered pairs in ‘R’. Then
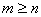
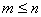
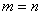
- none of these.
Q. 4. Let ‘X’ be a family of sets and ‘R’ be a relation defined by ‘A is disjoint from B’ .Then R is
- Reflexive
- Symmetric
- Anti symmetric
- Transitive
Q. 5. The number of surjections from A = {1, 2, 3, ….. n} on to B = {a, b} is
- nP2
- 2n - 2
- 2n - 1
- none
Q. 6. If a function 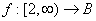 defined by f(x) = x2 - 4x + 5 is a bijection, then B =
defined by f(x) = x2 - 4x + 5 is a bijection, then B =
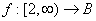 defined by f(x) = x2 - 4x + 5 is a bijection, then B =
defined by f(x) = x2 - 4x + 5 is a bijection, then B = - R
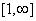
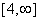
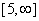
Q. 7. Let  be two functions given by f(x) = 2x - 3, g (x) = x3 + 5. fog-1(x) is equal to
be two functions given by f(x) = 2x - 3, g (x) = x3 + 5. fog-1(x) is equal to
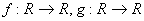 be two functions given by f(x) = 2x - 3, g (x) = x3 + 5. fog-1(x) is equal to
be two functions given by f(x) = 2x - 3, g (x) = x3 + 5. fog-1(x) is equal to
Q . 8. If A = { a, b} then the number of binary operations that can be defined on A is
- 4
- 2
- 16
- 1
Q. 9. Let f(x) = [x] and g(x) = x - [x] then which of the following function is the zero function
- (f+g) (x)
- (fg) (x)
- (f-g) (x)
- fog (x)
Q. 10. Let ‘A’ be a nonempty set and 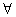 be a binary operator on
be a binary operator on 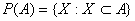 defined by
defined by  Identity element of the operator * is
Identity element of the operator * is
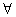 be a binary operator on
be a binary operator on 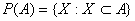 defined by
defined by  Identity element of the operator * is
Identity element of the operator * is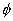
- A
- P(A)
- none
Q. 11. 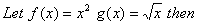
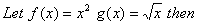
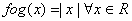
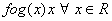
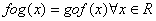
- none
Q. 12. Let f : R --> R be the signum function. g: R -> R g(x) = [x]. fog and gof coincides on [0, 1]. True/False?

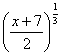
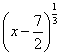
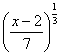
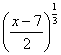

No comments:
Post a Comment