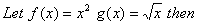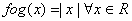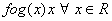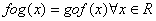Q. 1. If sin y = xcos(a + y) and 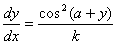 find k (3 marks)
find k (3 marks)
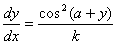 find k (3 marks)
find k (3 marks)
Q. 2. If f(x) = 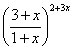 find f’(o) (3marks)
find f’(o) (3marks)
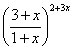 find f’(o) (3marks)
find f’(o) (3marks)
Q. 3. Verify the mean value theorem for f(x) = 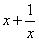 in [1,3] (4 marks)
in [1,3] (4 marks)
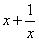 in [1,3] (4 marks)
in [1,3] (4 marks)
Q. 4. If x = a (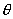 +
+ 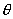 ) y = (1 + cos
) y = (1 + cos 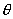 ) find
) find 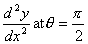 (4 marks)
(4 marks)
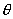 +
+ 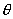 ) y = (1 + cos
) y = (1 + cos 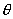 ) find
) find 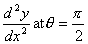 (4 marks)
(4 marks)
Q. 5. If xpyq = (x + y) p+q prove that 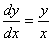
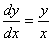
Or
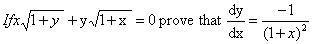 (4 marks)
(4 marks)
Q. 6. Consider the function defined as follows for 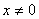 . In each case ,what choice (if any) of f(0) will make the function continuous at x = 0.
. In each case ,what choice (if any) of f(0) will make the function continuous at x = 0.
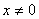 . In each case ,what choice (if any) of f(0) will make the function continuous at x = 0.
. In each case ,what choice (if any) of f(0) will make the function continuous at x = 0.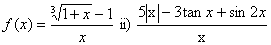 (4 marks)
(4 marks)
Q. 7. If x = acos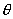 + bsin
+ bsin 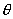 y = asin
y = asin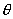 - bcos
- bcos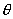
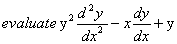 (4 marks)
(4 marks)
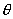 + bsin
+ bsin 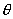 y = asin
y = asin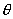 - bcos
- bcos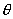
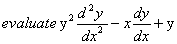 (4 marks)
(4 marks)
Q. 8.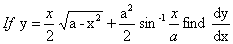
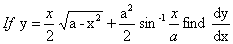
Or
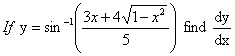 (4 marks)
(4 marks)- Construct a3 x 3 matrix A = [aij]whose elements are given by aij =
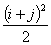 ( 3 marks)
( 3 marks) - Solve the matrix equation for x
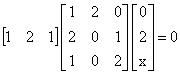 (3 marks)
(3 marks) - Solve the following equation for x
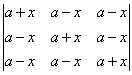 (3 marks)
(3 marks) - Prove that
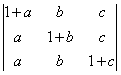 = a + b + c (3 marks)
= a + b + c (3 marks) - Solve the following equations for using matrices x - y + z = 4 2x + y -3z = 0 x + y + z = 2 ( 6 marks)
- Determinant of a skew symmetrix matrix of odd orderis always ( 1 marks)
a) zero
b) one
c) negative one
d) none - If A is a square matrix of order 3 then A.Adj (A) is (1 marks) a) | A | I3
b) | A | I2
C) | A | I
d) none

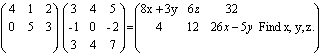
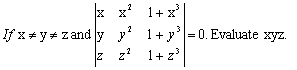
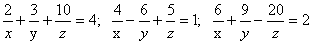
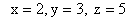
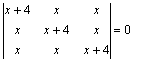
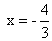
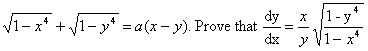
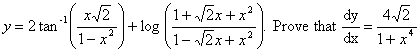

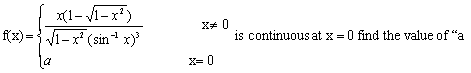
 The set S = {x: f(x) = f -1(x)} is
The set S = {x: f(x) = f -1(x)} is 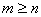
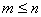
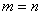
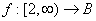 defined by f(x) = x2 - 4x + 5 is a bijection, then B =
defined by f(x) = x2 - 4x + 5 is a bijection, then B = 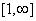
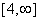
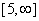
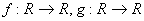 be two functions given by f(x) = 2x - 3, g (x) = x3 + 5. fog-1(x) is equal to
be two functions given by f(x) = 2x - 3, g (x) = x3 + 5. fog-1(x) is equal to 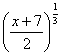
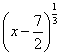
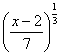
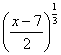
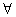 be a binary operator on
be a binary operator on 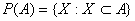 defined by
defined by  Identity element of the operator * is
Identity element of the operator * is